LES CHANGEMENTS MAJEURS QUE CES DECOUVERTES ONT PROVOQUES

. Le télescope de Newton :
            Après ses travaux sur la lumière, Newton est persuadé qu'il est possible d'améliorer la lunette astronomique de Galilée. En effet, celle-ci était fabriquée avec des lentilles qui déviaient la lumière. C'est ainsi qu'en 1672, Newton présente le télescope qui porte son nom à la Royal Society (c'est une association officielle des savants et mathématiciens). Son idée révolutionne alors la vie de l'époque.
            On se servait jusque là de la lunette astronomique de Galilée. La lentille utilisée rendait l'image floue : elle décomposait la lumière puisqu'elle la laissait passer. Cette lunette astronomique avait un grossissement maximum de 21.
            Newton, quant à lui, décida de remplacer cette lentille par un miroir concave. Il obtient alors une image nette sans effets de couleurs. La lumière est alors réfléchie par le miroir et non plus décomposée par la lentille. Ce télescope présente un avantage important : il ne mesure que 20 cm et permet de grossir jusqu'à 40 fois, soit le double de la lunette astronomique de Galillée. De plus, les miroirs étant moins chers que les lentilles, le télescope de Newton était plus accessible.
Cliquez ici pour voir le schéma du télescope de Newton

. L'impact de la méthode de Newton à l'époque :

          Dès la seconde moitié du XVIIe siècle, le domaine mathématique de l'analyse numérique connut une avancé prodigieuse. Newton était capable de formuler des théories mathématiques pour expliquer des faits connus à partir de nombreuses expériences qu’il a réalisées.
          La méthode des tangentes découle de l'une des théories mathématiques de Newton: celle des fluxions qu'il a inventée en octobre 1666. Ce terme est utilisé par Newton pour désigner ce qu’on appelle aujourd’hui la dérivée d’une fonction. Il s'est servi de ce mot car il considérait les quantités mathématiques comme engendrées par le mouvement: il cherchait le rapport des vitesses variables avec lesquelles ces quantités étaient décrites. Ce sont ces vitesses qu'il appelle fluxions des quantités. Il définira le concept de fluxions dans son œuvre La Méthode des fluxions qu’il ne publiera pas immédiatement.
          Cette méthode servira de base à ce qu'a conçu Leibniz en traitant la notion d'infiniment petit. En effet, Leibniz appelle une quantité différentielle(ou simplement différentielle), la différence infiniment petite de deux quantités finies, dont l’une surpasse l’autre infiniment peu. On obtient par conséquent une grandeur infiniment petite. Il exprime alors par la lettre  « d » la différence des quantités finies ; alors la différentielle de x est notée dx, celle de y, dy.
          C’est afin de montrer avec plus de facilité ce en quoi ces théories ont permis une avancée dans un premier temps à l’époque, que nous vous présentons des extraits de La Méthode des fluxions , que nous avons sélectionnés. Nous tenterons de les expliquer, en faisant un parallèle avec ce que nous savons à notre époque.

Voici un premier extrait :
          « On peut tirer les Tangentes différemment, selon les différentes relations des Courbes aux Lignes droites, et premièrement soit BD une Ligne droite Ordonnée sous un Angle donné à une autre Ligne droite AB prise pour Base ou Abscisse, et soit BD terminée à une Courbe ED. Faites mouvoir cette Ordonnée et faites lui parcourir un Espace infiniment petit et parvenir à bd. Elle aura augmenté du Moment cd, tandis que AB aura augmenté du Moment Bb auquel Dc est égal et parallèle. Prolongez Dd jusqu'à ce qu'elle rencontre AB en T, cette Ligne touchera la Courbe en D ou d, et les Triangles dcD, DBT seront semblables, ce qui donne TB:BD::Dc ou Bb: cd. ( en notations contemporaines, TB/DB=Dc/cd= Bb/cd). »
(La méthode des Fluxions, page 49)

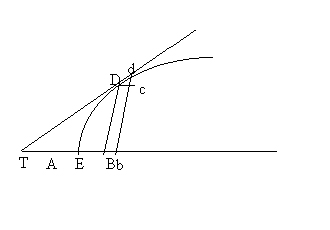
          Ici, les lignes droites sont l’abscisse et l’ordonnée usuelles. Il considère ensuite un déplacement " infiniment petit " de D en d et les " moments " comme une fluxion, c'est-à-dire l’accroissement momentané d’une quantité. Newton veut montrer que :
- deux points infiniment voisins (ici D et d) continuent à déterminer une droite, s’ils sont distincts.
- si d est infiniment voisin de D sur la courbe, la droite Dd est tangente à la courbe " en D ou d ". Ceci implique que tous les points de la courbe infiniment voisins de D sont sur la tangente (ici DT) à la courbe.
          Cet extrait de Newton correspond en fait à l’approximation comme expliqué dans la partie précédente. On peut alors imaginer un point M dont l’abscisse est la variable t et un point M’ correspondant  à t+h avec h infiniment petit. Newton, à l’exemple de l’approximation, considère que la droite (Dd), dans notre exemple (MM’) coïncide avec la courbe Dd, pour nous la courbe entre M et M’ et représente la tangente.
          L’approximation de Newton dans la méthode des fluxions a permis, dans un premier temps la construction des tangentes à une courbe puis le calcul de leur coefficient directeur.
Dans un second temps, cela a permis la progression de l'avancement d'outils mathématiques en introduisant la limite d'une grandeur. Suite à la définition de la limite, il a été possible, par exemple, d'avancer dans la construction de l'ensemble du réel R.


Voici un second extrait :
« Reste maintenant à donner quelques essais de problèmes, surtout ceux que nous présente la nature des courbes, et cela pour mettre l'art analytique dans un plus grand jour. Et d'abord j'observerai que toutes leurs difficultés peuvent se réduire à ces deux problèmes seulement que je vais proposer sur un espace décrit par un mouvement local retardé ou accéléré de façon quelconque.
1. La longueur de l’Espace décrit étant continuellement donnée, trouver la vitesse du Mouvement à un temps donné quelconque.
2. La vitesse du Mouvement étant continuellement donnée, trouver la longueur de l’Espace décrit à un temps donné quelconque. »

          Newton ici relève deux problèmes qu’il a entreprit : la résolution de la dérivation à laquelle la méthode des tangentes est la solution et l’intégration, cependant à considérer uniquement si la variable est le temps.
          La résolution de l‘intégration a été permise par la généralisation des méthodes déjà utilisées de Newton. Elle a été utilisé, par exemple, dans le calcul de surfaces délimitées par une courbe, qui est introduit par le calcul différentiel et intégral (ou infinitésimal). La compréhension de cette nouveauté apportée n’étant plus de notre niveau, nous ne pouvons que nous résoudre à vous montrez le schéma ci-contre qui en montre le résultat, sans plus de détails.

          Comme mentionné plus tôt une progression d’outils mathématiques a été favorisée.  Cela  a contribué à l’approfondissement de la méthode de Newton, qui a servi non seulement à relever des questions mathématiques et par la même occasion, à résoudre certaines soulevés dans le domaine de la physique.