LA METHODE DES TANGENTES

            Newton a proposé une méthode générale pour calculer numériquement l’approximation d’une racine d'une fonction. Décrite pour la première fois par le mathématicien anglais en 1669 dans son œuvre De analysi per aequationes numero terminorum infinitas, la méthode de Newton (également appelée « méthode des tangentes ») consiste à choisir initialement une valeur, à calculer la tangente du polynôme en cette valeur, à trouver la racine de la tangente et à réitérer.
L'idée est de remplacer la courbe représentative de la fonction par une tangente étant donné que la tangente en un des points de cette courbe est une droite qui la « touche » au plus près du voisinage de ce point. La courbe et sa tangente forment alors un angle nul en ce point. Les directions de la tangente et de la courbe seront donc très proches. Géométriquement, voici les étapes à suivre :

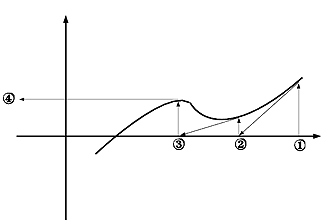
            On part d'un point x0 de l'ensemble de définition de f de préférence assez proche du zéro que l’on souhaite trouver, et on considère que la fonction est à peu près égale à la tangente en ce point (x0,f(x0)) :
(fx) ≈ f(x0) + f '(x0)(x − x0)
Partant de là, pour trouver une approximation du zéro, il faut trouver l’intersection de la tangente avec l’axe des abscisses ; c’est-à-dire qu’il faut résoudre l’équation : f(x0) + f '(x0)(x − x0) = 0
            Soit x1 l'abscisse de l'intersection de la tangente avec l'axe des abscisses. Puisque la tangente est proche de la courbe, on peut espérer que x1 donne une meilleure estimation d'une solution de l'équation f(x)=0 que x0. On recommence alors le procédé à partir de x1 afin d’obtenir x2, etc... C’est-à-dire que chaque nouvelle tangente commence là où la précédente coupait l’axe des abscisses. Chaque répétition du processus (itération) permet de rapprocher de plus en plus la ligne tangente de la racine. On va ainsi pouvoir trouver une approximation de cette dernière.
            Pour appliquer cette méthode, il faut donc que la fonction soit dérivable puisqu’elle requiert que la fonction possède une tangente en chacun des points de l’on utilise.

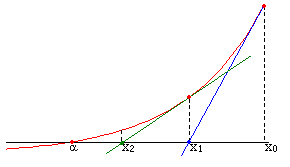
            Il faut cependant savoir que cette méthode peut échouer et ainsi donner des résultats aberrants si l'on considère un point x0 trop éloigné de la racine que l'on souhaite étudier. Dans ce cas-là, l'intervalle de recherche, plus large, pourrait inclure un extrémum local. Or, si par itération il faut dériver et donc tracer la tangente en ce point particulier de la courbe, la tangente obtenue sera horizontale puisque f '(x) = 0 lorsque f admet un extrémum local. Cette dernière tangente ne va donc pas couper l'axe des abscisses et par conséquent, il n'y aura pas d'approximation correcte de la racine. Voici ci-dessous un exemple de cas particulier où la méthode échoue (cliquez sur l'image pour l'agrandir):
            D’un point de vue plus mathématique, la méthode revient à résoudre l’équation suivante (dites la formule de Raphson-Newton):
xn+1 = xn + [ f(xn) / f '(xn) ]  où xn+1 est la solution de l’équation f(x0) + f '(x0)(x − x0) = 0 et où f ' est la dérivée de la fonction f.